Data Structures
Contents
Data Structures#
Data structures allow us to speed up our algorithms often by many orders of magnitude. They arrange the data in a way that is suitable for the problem and usually simplify the workings of the algorithm. In this notebook, we will implement some of the most popular data structures in computer science:
Array#
Arrays are lists of objects. In some programming languages, arrays are objects of fixed length and have a type (e.g. list of 10 integers). In Python, are implemented using lists, which provide a little more flexibility by hosting multiple types and variable length. Arrays/lists support the following operation in complexity:
Set item (at index i smaller than the length): \(O(1)\)
Get item: \(O(1)\)
Deletion is no really supported as we assume that the array is of fixed length, for Python lists it is \(O(n)\).
Arrays are used in many programming problems where collections of data show up.
arr = [1,2,3]
# constant
arr[2] = 4
# constant
print(arr[1])
2
Stack#
A stack is a structure that follows that LIFO (last in, first out) rule. Elements can be pushed on top of the stack or popped of it. Those are the only two operations that this structure supports:
class Stack:
def __init__(self):
self.contents = []
def pop(self):
if len(self.contents):
temp = self.contents[-1]
self.contents = self.contents[:-1]
return temp
else:
print("ERROR: Stack is empty")
def push(self, elem):
self.contents.append(elem)
st = Stack()
st.push(1)
print(st.pop())
st.pop()
# Python lists also support these operations, push is called append!
l = [1,2]
print(l.pop())
l.append(3)
print(l)
1
ERROR: Stack is empty
2
[1, 3]
Operations/complexity:
push: \(O(1)\)
pop: \(O(1)\)
One of popular problems utilizing stacks is checking whether an expression has balanced brackets. Let us limit ourselves to expressions consisting of [{,},(,)]. We will push the opening brackets on the stack and pop them when the closing bracket is approached. Of course, the types of brackets must match:
def checkIfValidBracketing(expr):
# our stack :)
st = []
for i in expr:
# not a bracket
if i not in ["{","}","(",")"]:
continue
# push the opening bracket on the stack
elif i in ["{","("]:
st.append(i)
# check when closing bracket approached
elif i in ["}",")"]:
try:
temp = st.pop()
if (i == "}" and temp == "{") or (i == ")" and temp == "("):
continue
# invalid bracketing
else:
return False
except IndexError:
return False
return not len(st)
# Basic testing
print("{}()",checkIfValidBracketing("{}()"))
print("{(",checkIfValidBracketing("{("))
print("({()})",checkIfValidBracketing("({()})"))
print(")",checkIfValidBracketing(")"))
print("",checkIfValidBracketing(""))
{}() True
{( False
({()}) True
) False
True
The following algorithm has \(O(n)\) time and space complexity.
Linked list#
Linked lists are the simplest node-based structures. They are inherently recursive. A linked list consists of a head pointing to the next which itself is a linked list. The base case is an empty list:

A simple implementation would be:
class Node:
def __init__(self,val):
self.val = val
self.next = None
class LinkedList:
def __init__(self):
self.head = None
# insert at a position index
# false is index out of range, true otherwise
def insert(self,x, index):
assert index >= 0
newNode = Node(x)
if not index:
newNode.next = self.head
self.head = newNode
return True
else:
curr = self.head
for _ in range(index-1):
if curr is None:
return False
curr = curr.next
if curr is None:
return False
newNode.next = curr.next
curr.next = newNode
return True
# remove item at index position
# return true if the element was actually removed,
# false otherwise
def remove(self,index):
assert index >= 0
# Removing head
if not index:
if self.head is not None:
self.head = self.head.next
return True
else:
return False
# index > 0
else:
curr = self.head
for _ in range(index-1):
if curr is None:
return False
curr = curr.next
if curr is None:
return False
else:
if curr.next is None:
return False
else:
curr.next = curr.next.next
return True
# returns true if x in the list, false otherwise
def search(self,x):
curr = self.head
while curr is not None:
if curr.val == x:
return True
curr = curr.next
return False
# for testing and nice representation
def __str__(self):
res = ""
curr = self.head
while curr is not None:
res += str(curr.val) + "->"
curr = curr.next
return res
ll = LinkedList()
print(ll)
print(ll.insert(0,0))
print(ll)
print(ll.insert(1,1))
print(ll)
print(ll.insert(2,1))
print(ll)
print(ll.remove(2))
print(ll)
print(ll.search(2))
print(ll.remove(0))
print(ll)
print(ll.search(0))
print(ll.remove(0))
print(ll.remove(0))
True
0->
True
0->1->
True
0->2->1->
True
0->2->
True
True
2->
False
True
False
All of these operations (insert,remove,search) take \(O(n)\) which is usually not optimal. There are numerous versions of linked lists e.g. doubly linked list which has nodes that point both to the previous and next nodes. Linked lists are often used to implement other data structures such as queues.
Queue#
Ques are similar to stacks but utilize the FIFO (first in, first out) rule. Basic ques support enqueue and dequeue operations. A linked list implementation would be:
class Node:
def __init__(self, item):
self.item = item
self.next = None
self.previous = None
class Queue:
def __init__(self):
self.length = 0
self.head = None
self.tail = None
def enqueue(self, x):
newNode = Node(x)
if self.head == None:
self.head = self.tail = newNode
else:
self.tail.next = newNode
newNode.previous = self.tail
self.tail = newNode
self.length += 1
def dequeue(self):
if not self.length:
return None
item = self.head.item
self.head = self.head.next
self.length -= 1
if self.length == 0:
self.tail = None
return item
def __str__(self):
res = ""
curr = self.head
while curr is not None:
res += str(curr.item) + "->"
curr = curr.next
return res
queue = Queue()
print(queue)
queue.enqueue(1)
queue.enqueue(2)
queue.enqueue(3)
print(queue)
print(queue.dequeue())
print(queue)
print(queue.dequeue())
print(queue)
print(queue.dequeue())
print(queue)
print(queue.dequeue())
1->2->3->
1
2->3->
2
3->
3
None
With this implementation enqueue and dequeue are \(O(1)\). Queues are used in numerous problems, such as graph traversals (BFS).
Binary search tree (BST)#
Binary tree is another node-based structure also recursive in nature. The tree consists of a root which points to at most two children which are also binary trees. Binary search trees are a type of binary trees which have the property that the key of the left child is no greater than the root key. Right child’s key is greater than the root key. An example binary search tree is as follows:
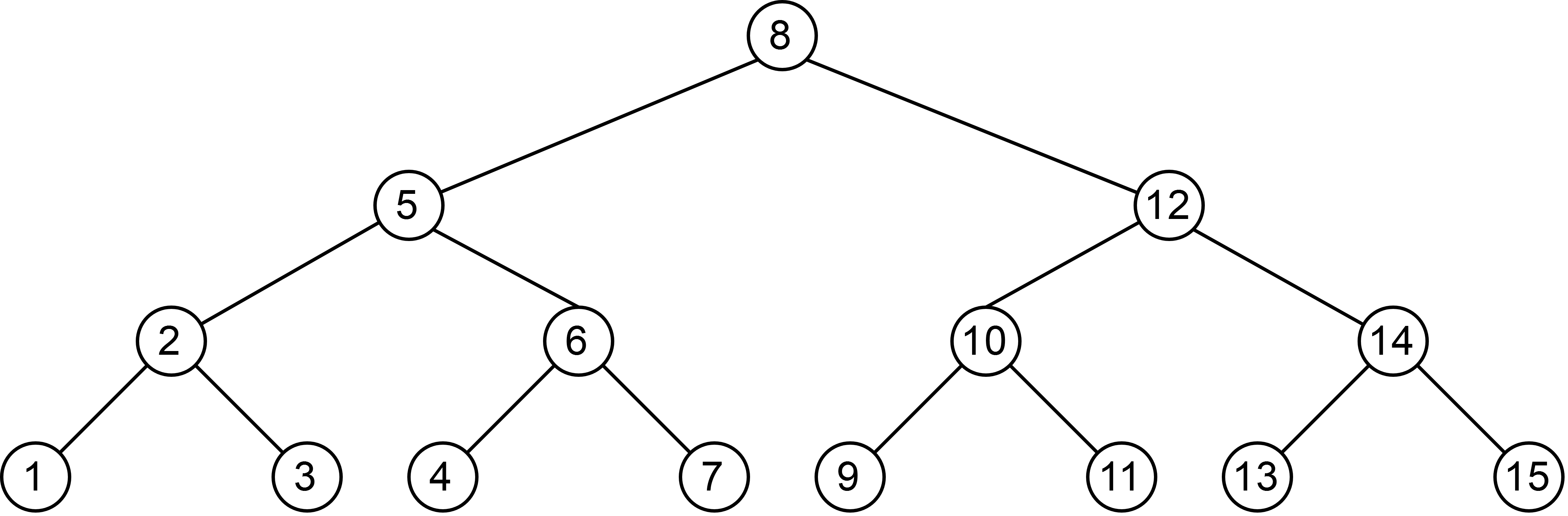
An example implementation for BST with integers is as follows:
# implemented as a set, will not contain duplicates
class BST:
def __init__(self,val=None):
self.val = val
self.left = None
self.right = None
# true if the insert changes the BST
def insert(self,x):
if self.val is None:
self.val = x
return True
# already in the set
elif self.val == x:
return False
elif self.val > x:
if self.left is None:
self.left = BST(x)
return True
else:
return self.left.insert(x)
else:
if self.right is None:
self.right = BST(x)
return True
else:
return self.right.insert(x)
# seach for x in BST
def search(self,x):
if self.val is None:
return False
elif self.val == x:
return True
elif self.val > x:
if self.left is None:
return False
else:
return self.left.search(x)
else:
if self.right is None:
return False
else:
return self.right.search(x)
Node removal is a bit more involved and will not be covered. All basic operations can be done in \(O(\log(n))\). BST can be used to speed up many problems that require repetitive searching of the data. Consider the following problem:
Numbers smaller than the given number in an array You are given an array of integers. You should provide a data structure which should return the number of elements smaller than any chosen element in the array.
We will solve the question by constructing a BST out of the array that will store the the number of nodes to the left of the node (its rank):
class newNode:
def __init__(self, data):
self.data = data
self.left = self.right = None
self.leftSize = 0
# Inserting a new Node.
def insert(root, data):
if root is None:
return newNode(data)
# Updating size of left subtree.
if data <= root.data:
root.left = insert(root.left, data)
root.leftSize += 1
else:
root.right = insert(root.right, data)
return root
# Function to get Rank of a Node x.
def getRank(root, x):
if root.data == x:
return root.leftSize
if x < root.data:
if root.left is None:
return -1
else:
return getRank(root.left, x)
else:
if root.right is None:
return -1
else:
rightSize = getRank(root.right, x)
if rightSize == -1:
# x not found in right sub tree, i.e. not found in stream
return -1
else:
return root.leftSize + 1 + rightSize
arr = [5, 1, 4, 4, 5, 9, 7, 13, 3]
root = None
for i in range(len(arr)):
root = insert(root, arr[i])
print(getRank(root, 4))
print(getRank(root, 13))
print(getRank(root, 8))
3
8
-1
This algorithm will work in \(O(\log(n))\) time on average. However, of the array was initially sorted the formed tree will be degenerate (it will form a linked list). We will learn how to solve such cases in AVL trees.
Heap#
Heaps (especially binary heaps) are tree-like structures that have two properties:
They are a complete tree (all levels of the tree are filled except possibly the last level).
It is either a min-heap or a max-heap. In the first case, the root is smaller or equal to its children. The opposite is true for the max heap.
Let us implement a min-heap storing integers. It will support taking the top element (which is the minimum) as well as inserting new elements. Interestingly, we will implement it using a Python list. It is an important fact to spot that a parent of an element at index i is at index i//2.
# utility functions
def swap(arr, x, y):
temp = arr[x]
arr[x] = arr[y]
arr[y] = temp
class MinHeap:
def __init__(self):
self.contents = []
self.size = 0
# utility function
def heapifyUp(self, i):
while i // 2 > 0:
if self.contents[i-1] < self.contents[i // 2 - 1]:
swap(self.contents, i-1, i // 2 - 1)
i //= 2
def insert(self,val):
self.size += 1
self.contents.append(val)
self.heapifyUp(self.size)
def heapifyDown(self,i):
while (2 * i + 1) < self.size:
mc = self.minChild(i)
if self.contents[i] > self.contents[mc]:
swap(self.contents, i, mc)
i = mc
def minChild(self, i):
if 2 * i + 2 >= self.size:
return 2 * i + 1
else:
if self.contents[2 * i + 1] < self.contents[2 * i + 2]:
return 2 * i + 1
else:
return 2 * i + 2
def getMin(self):
assert self.size > 0
self.size -= 1
res = self.contents[0]
swap(self.contents,0, self.size)
self.contents.pop()
self.heapifyDown(0)
return res
#Heapsort - a O(nlog(n)) sorting algorithm.
arr = [1,3,2,6,8,3,4,5,6,7,2,3,8]
heap = MinHeap()
for j in range(len(arr)):
heap.insert(arr[j])
print(heap.contents)
arr = []
while heap.size:
arr.append(heap.getMin())
print(arr)
[1, 2, 2, 5, 3, 3, 4, 6, 6, 8, 7, 3, 8]
[1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 7, 8, 8]
Heaps have many, many uses. One of such is HeapSort - a \(O(n\log(n))\) sorting algorithm (see above). Heaps are also used in priority queues - queues which have the elements sorted by some priority such as objects sorted by their value.
AVL Tree#
Consider the case we insert a sorted list into a regular BST. We would end up with the following structure:
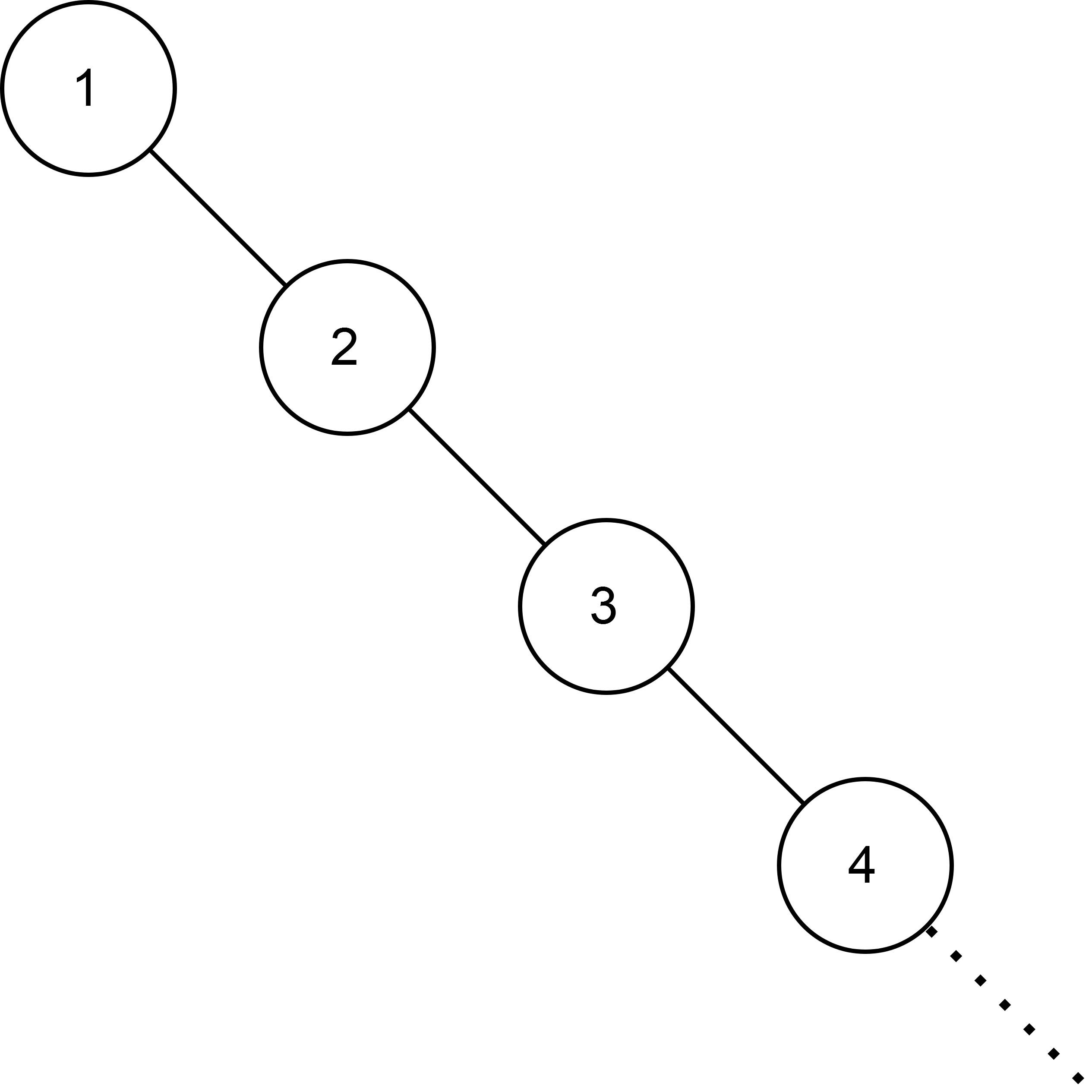
This tree is degenerate. Search operations are \(O(n)\) which is too slow for many implementations. To counter the degeneration we can utilize self-balancing binary trees such as the AVL tree (named after Adelson-Velsky and Landis). This type of tree holds the invariant that for each node the difference in heights between left and right subtree is at most 1. Let us see how it is achieved.
AVL insertion#
The first stage of insertion is the same as in BST, we recurse down the tree until we find an appropriate spot for the new value.
Each node in the AVL tree has a height (the distance between the node and the farthest leaf node in the children). We check if the difference in heights of children exceeds 1 in absolute value. If so, the tree is imbalanced. Such violation can occur in four possible ways (see the diagram below). We will use node rotations to solve the problem:
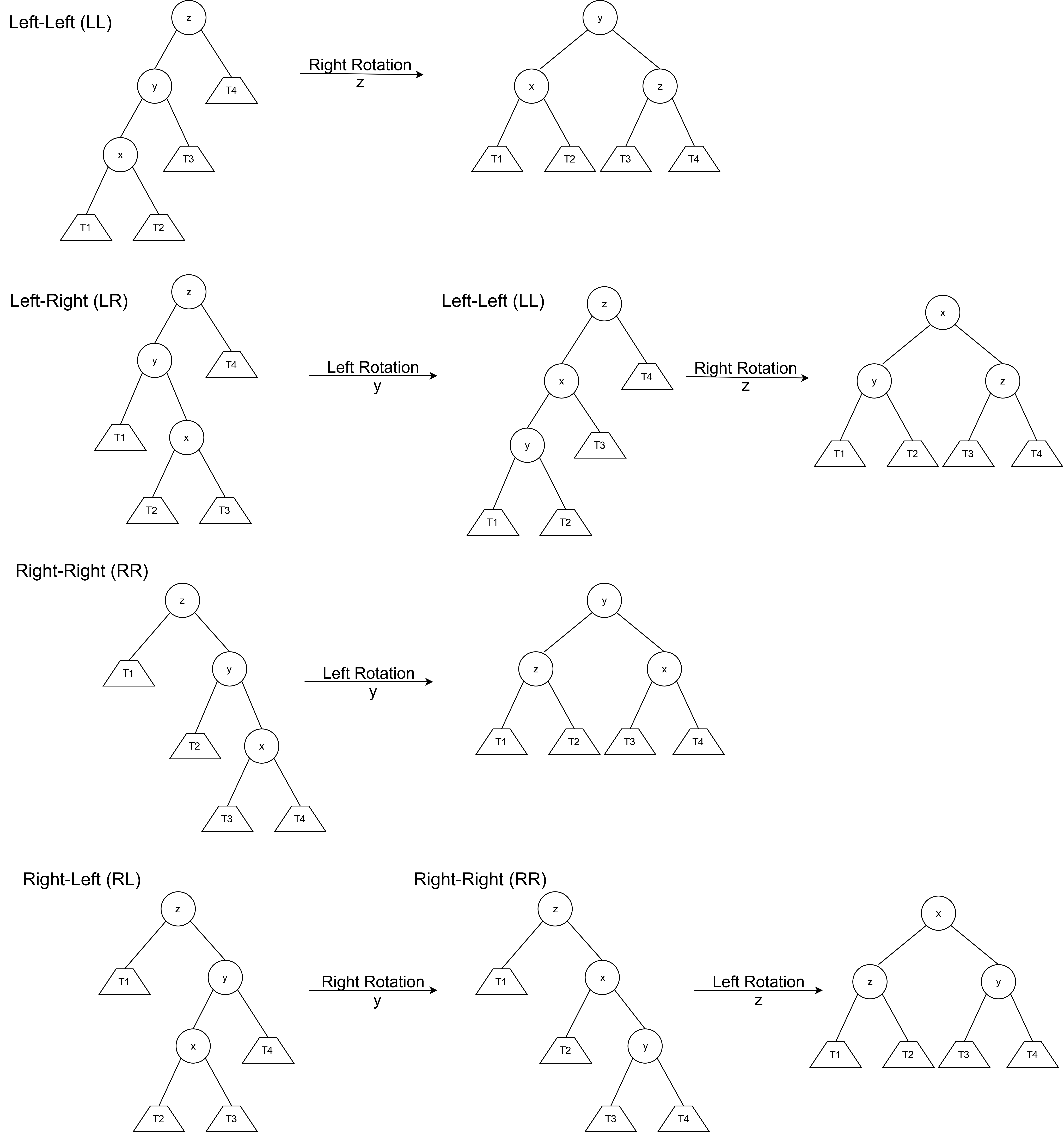
The implementation of the AVL tree is presented below, please take a while to digest it. The topic is not trivial. Also, have a look at the comparison between the BST and AVL in the degenerate case:
import time
# we will support only insertions and deletions
class AVLNode:
# has to be initialised with a root value
def __init__(self,val):
self.val = val
self.left = None
self.right = None
self.height = 0
# searching is the same as in regural BST
def search(self,val):
if val == self.val:
return True
elif val < self.val:
if self.left is not None:
return self.left.search(val)
else:
return False
else:
if self.right is not None:
return self.right.search(val)
else:
return False
def insert(self, root, val):
# Normal BST insert
if not root:
return AVLNode(val)
elif root.val == val:
return root
elif val < root.val:
root.left = self.insert(root.left,val)
else:
root.right = self.insert(root.right,val)
# update the height of the root
root.height = 1 + max(getHeight(root.left), getHeight(root.right))
# get the balance factor
balance = getBalance(root)
# consider 4 cases
# LL
if balance > 1 and val < root.left.val:
return rotateRight(root)
# RR
if balance < -1 and val > root.right.val:
return rotateLeft(root)
# LR
if balance > 1 and val > root.left.val:
root.left = rotateLeft(root.left)
return rotateRight(root)
# RL
if balance < -1 and val < root.right:
root.right = rotateRight(root.right)
return rotateLeft(root)
return root
# UTILITY FUNCTIONS
#_____________________________________________
# how is the tree unbalanced?
def getBalance(node):
if not node:
return 0
else:
return getHeight(node.left) - getHeight(node.right)
# get height of a node
def getHeight(node):
if not node:
return 0
else:
return node.height
def rotateRight(node):
# do the rewiring
z = node
y = z.left
T3 = y.right
y.right = z
z.left = T3
# update heights
z.height = 1 + max(getHeight(z.left),
getHeight(z.right))
y.height = 1 + max(getHeight(y.left),
getHeight(y.right))
return y
def rotateLeft(node):
# do the rewiring
z = node
y = z.right
T2 = y.left
y.left = z
z.right = T2
# update heights
z.height = 1 + max(getHeight(z.left),
getHeight(z.right))
y.height = 1 + max(getHeight(y.left),
getHeight(y.right))
return y
#_____________________________________________
# Change the code below according to your preference
arr = list(range(1000))
t = time.time()
bst = BST(0)
avl = AVLNode(0)
for i in arr:
bst.insert(i)
bst.search(i)
print("BST time:",time.time() - t)
t = time.time()
for i in arr:
avl = avl.insert(avl, i)
avl.search(i)
print("AVL time:", time.time() - t)
print("Height of the AVL Tree: " + str(avl.height))
BST time: 0.538590669631958
AVL time: 0.014953136444091797
Height of the AVL Tree: 10
Hash Table#
In simple terms, a hash table is identical to Python dict dictionaries. They allow us to retrieve objects (given their key) in \(O(1)\) time on average. They also allow for constant time insertion and deletion. Wait, what? Does it mean that they are ultimately the fastest data structures? - as you can probably guess it is not that simple. It will become clear as we will implement a simple hash table:
A hash table is similar to an array. It has some fixed capacity which can be changed (not in constant time). The elements are indexed by the key values. For the hash table to work, the elements need to be indexed by integer values. A special function, called the hash function transforms the key values to integers. The basic utilities needed by a hash table are shown in the class below:
class HashTable:
def __init__(self,size = 8):
pass
#Insert a new key-value pair or overwrite an existing one
def insert(self,key, value):
pass
# Overload the [] index access
def __setitem__(self,key,value):
return self.insert(key,value)
# Retreive the value given the key
def get(self, key):
pass
# Overload the [] index access
def __getitem__(self,key):
return self.get(key)
# Computes the hash position
def _hash(self,key):
pass
Hash function#
First, we will choose a hash function which will map keys to particular positions in the array. There are multiple ways of approaching this problem. Two simple ones include:
The mod method In this case, we take the remainder of dividing the key by the table-size:
h(key) = key % table_size
This is a very fast hash function. However, many keys can have the same hash which results in collisions (e.g. 64 % 8 and 8 % 8 are both 0). We discuss those below.
The multiplication method First we multiply the key by
0 < c < 1and take the fractional part ofk * cwhich isk * c - floor(k * c). This method leads to fewer overlaps and therefore we will use it in our implementation. Some values ofcwork better statistically.c ~ (sqrt (5) – 1) / 2is likely to work well.
h(key) = floor(table_size * (key * c - floor(key * c)))
Both of these functions can lead to inefficient hash tables with operations with \(O(n)\) worst-case time. There are more advanced methods which solve this problem, which you are free to research here.
Overlaps#
When two different keys are mapped to the same hash value we are dealing with an overlap. The way our implementation will tackle this problem is by chaining. Each entry in the table will be a linked list-like object. In case of an overlap, we will append at the end of such a list. Of course, in the case when all elements collide we will one big linked-list object. The role of our hash function is to minimise the probability of this happening.
Doubling#
Let n denote the number of elements in the hash table. The load factor is defined as n / table_size. As our table becomes more filled more cells (on average) become linked lists. To counter this effect we will double the size of the table when the load factor reaches a certain value (in our case \(1\)). We will not support deletion therefore shrinking is not essential.
With all this knowledge let us provide an implementation:
import math, random
# We will support string keys
# it could be easily translated to integer keys
# the table will be a 2d array of tuples (key,value)
class HashTable:
def __init__(self,size = 8):
self.contents = []
self.size = size
self.load = 0
for _ in range(self.size):
self.contents.append([])
#Insert a new key-value pair or overwrite an existing one
def insert(self,key, value):
elem = (key, value)
# calculate the hash value
hashVal = self._hash(key)
# insert the element (chaining)
# check in elem already in
if elem not in self.contents[hashVal]:
self.contents[hashVal].append(elem)
# increase the load
self.load += 1
# doubling
if self.load / self.size > 1:
# double the size
self.size *= 2
# make new contents table
newContents = []
for _ in range(self.size):
newContents.append([])
# insert the old elements
for i in self.contents:
for j in i:
hashVal = self._hash(j[0])
# insert the element (chaining)
newContents[hashVal].append(j)
self.contents = newContents
# Overload the [] index access
def __setitem__(self,key,value):
return self.insert(key,value)
# Retreive the value given the key
def get(self, key):
hashVal = self._hash(key)
for i in self.contents[hashVal]:
if i[0] == key:
return i[1]
print("Key has no value associated")
# Overload the [] index access
def __getitem__(self,key):
return self.get(key)
# Computes the hash position
def _hash(self,key):
k = sum(ord(c) for c in key)
c = (math.sqrt(5) - 1) / 2
return min(math.floor(self.size * (k * c - math.floor(k * c))),self.size - 1)
# Testing out
ht = HashTable()
for _ in range(16):
temp = ''
for i in range(random.randint(1,5)):
temp += chr(random.randint(ord('a'),ord('z')))
ht[temp] = random.randint(0,17)
print(ht[temp])
print(ht.contents)
4
7
4
0
6
4
3
1
11
8
7
3
17
8
5
5
[[], [], [('lemo', 3), ('emz', 5)], [], [('ps', 0)], [('sdens', 4), ('jbzni', 3)], [('jcpgq', 17)], [('zjb', 7)], [('w', 4), ('cbl', 8)], [], [], [], [('xsfj', 5)], [('po', 7), ('sazku', 4), ('udl', 1), ('vv', 8)], [('i', 11)], [('n', 6)]]
References#
Cormen, Leiserson, Rivest, Stein, “Introduction to Algorithms”, Third Edition, MIT Press, 2009
GeeksforGeeks, Rank Elements in an Integer Stream (BST)
Pythonds, Binary Heap Implementation
GeeksforGeeks, AVL Insertion
Sebastian Raschka, Github, Implementing a Simple Hash Table
GeeksforGeeks, Implementation of Hashing with Chaining in Python

