Reading Maps

Tectonics of the Ocean Remote Sensing Earth and Planets

import numpy as np
import matplotlib.pyplot as plt

Latitude

Latitude is the angular distance of a place north or south of the earth’s equator, or of the equator of a celestial object, usually expressed in degrees, minutes and seconds.

\(1\) degree latitude is about \(111\,km\) anywhere on earth.

Lines of latitude are numbered from \(0°\) at the equator to \(90°N\) or \(+90\) at the North Pole. Lines of latitude are numbered from \(0°\) at the equator to \(90°S\) or \(-90\) at the South Pole.

plt.figure()
plt.subplot(111, projection="mollweide")
plt.title("Latitude")
plt.grid(True, axis='y')

Longitude

The distance of \(1\) degree longitude varies from \(111\,km\) at equator to \(0\) at poles, half way approx. = \(55.8\,km\) at \(60\) degrees latitude.

Longitude varies as \(\cos \theta\), where \(\theta\) is the latitude (e.g. long at \(80°N = 111\cos(80°) = 19\,km\))

Lines of longitude begin at the Prime Meridian (Greenwich).

\(60°W\) is the \(60°\) line of longitude west of the Prime Meridian. Is also written as \(-60°\)

\(60°E\) is the \(60°\) line of longitude east of the Prime Meridian. Is also written as \(+60°\)

Sometimes you will see longitude on a scale \(0°\) to \(360°\). The scale is measured clockwise (so \(10°W == 350° == -10°\))

plt.figure()
plt.subplot(111, projection="mollweide")
plt.title("Longitude")
plt.grid(True, axis='x')

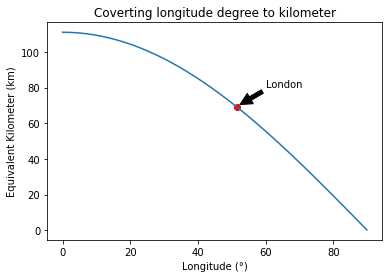
# Plot to covert the distance of 1 degree at a certain longitude to kilometer

x = np.arange(0, 90, 0.1)
y = 111*np.cos(x*(np.pi)/180)

plt.plot(x, y)
plt.scatter(51.5, 111*np.cos(51.5*(np.pi)/180),color='r')
plt.annotate('London', xy=(52, 70), xytext=(60, 80),
             arrowprops=dict(facecolor='black', shrink=0.05),
             )
plt.title("Coverting longitude degree to kilometer")
plt.xlabel('Longitude (°)')
plt.ylabel('Equivalent Kilometer (km)')
plt.show()

# The distance of 1 degree at a certain longitude to kilometer convertion
def longitude_km_convertion(longitude):
    longitude_km = 111*np.cos(longitude*(np.pi)/180)
    return longitude_km

print(f'The distance of 1 degree at 80°N is equal to {round(longitude_km_convertion(80),2)} km.')

The distance of 1 degree at 80°N is equal to 19.27 km.

Degree Notation

One degree is equal to \(60\) minutes and equal to \(3600\) seconds:

\[ 1° = 60' = 3600'' \]

One minute is equal to \(1/60\) degrees:

\[1' = (1/60)° = 0.01666667°\]

One second is equal to \(1/3600\) degrees:

\[1'' = (1/3600)° = 2.77778e-4° = 0.000277778°\]

# Degree notation to decimal degree convertion
def decimal_degree_covertion(degree, minute, second):
    decimal_degree = degree + minute/60 + second/3600
    return decimal_degree

print(f'53° 30\' 36" is equal to {decimal_degree_covertion(53, 30, 36)}°.')

53° 30' 36" is equal to 53.51°.

Reference

2022 notes and practical from Lecture 1 of the module ESE 60028 Tectonics of the Ocean