Gravity

Mechanics Physical Processes

Newton’s Law of Universal Gravitation

The gravitational force \(F\) that body \(A\) exerts on body \(B\) has a magnitude that is directly proportional to the mass of body \(A\) \((m_a)\) and the mass of body \(B\) \((m_b)\), and inversely proportional to the square of the distance between their centres \(R\).

Mathematically:

\[F=\frac{Gm_am_b}{R^2}\]

where \(G\) is the gravitational constant, equal to \(6.674\times 10^{-11}\,N\,m^2kg^{-2}\).

Therefore, the gravitational force exerted on a mass \(m\) by a planet of mass \(m_p\) is:

\[F=\frac{Gm_pm}{R_p^2}\]

where \(m_p\) and \(R_p\) is the mass and radius of a planet respectively.

The local gravitational acceleration \(g\) is:

\[a=\frac{F}{m}=\frac{Gm_p}{R_p^2}=g\]

In terms of density \(\rho\):

\[g=\frac{4\pi\rho R_p^3G}{3R_p^2}=\frac{4\pi\rho R_pG}{3}\]

Gravitational Potential Energy

The definition of change in energy is that a force \(F\) moves a body from position 1 \(R_1\) to position 2 \(R_2\). In the case of change in gravitational potential energy \(GPE\) on Earth:

\[F=-\frac{Gm_Em}{R^2}\]

where \(m_E\) and \(R\) are the mass of the Earth and distance from Earth’s centre respectively,

\[GPE_2-GPE_1=-\int_{R_1}^{R_2}F(R)\,dR=Gm_Em\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\]

Taking \(R_2\) to be infinitely far away from the Earth:

\[GPE(\infty)-GPE(R_1)=Gm_Em(\frac{1}{R_1}-0)=\frac{Gm_Em}{R_1}\]

Rearranging for \(GPE(R_1)\):

\[GPE(R_1)=-\frac{Gm_Em}{R_1}\]

For a body at an elevation \(h\) close to the surface, \(GPE\) is roughly equal to \(mgh\).

Escape Velocity

To fully escape the gravitational field of a planet, the object must reach “infinity” where \(GPE=0\). Thus, taking position 2 as infinity:

\[KE(1)+GPE(R_E)=KE(2)+GPE(\infty)\]

To find the minimum velocity required, we set \(KE(2)=0\), and since \(GPE(\infty)=0\):

\[KE(1)+GPE(R_E)=0\]

\[\frac{mv_e^2}{2}-\frac{Gm_Em}{R_E}=0\]

Rearranging for escape velocity \(v_e\):

\[v_e=\sqrt{\frac{2Gm_E}{R_E}}\]

Maxwell-Boltzmann distribution

At absolute temperature \(T\), the mean energy of monoatomic molecules is given by:

\[\frac{3}{2}k_BT\]

where \(k_B\) is the Boltzmann’s constant equal to \(1.38\times10^{-23}\,m^2kg\,s^{-2}K^{-1}\).

Ignoring potential energy and assuming that the energy of the monoatomic molecules is only from their kinetic energy, we can equate the above equation with the kinetic energy equation:

\[\frac{mv_{mean}^2}{2}=\frac{3}{2}k_BT\]

where \(m\) is the mass of that monoatomic molecule, and \(v_{mean}\) is the mean velocity of the monoatomic molecules at temperature \(T\).

Rearranging for \(v_{mean}\):

\[v_{mean}=\sqrt{\frac{3k_BT}{m}}\]

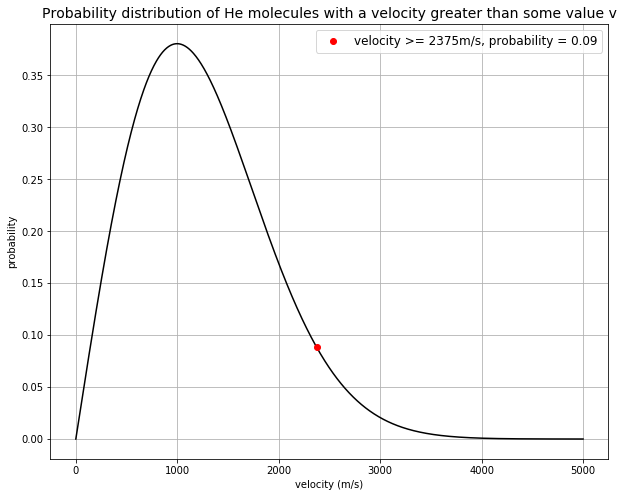
The probability of a molecule having a velocity higher than some value \(v\) is given by:

\[\frac{v}{v_{mean}}e^{-1.27\left(\frac{v}{v_{mean}}\right)^2}\]

Tutorial Problem 5.3

What is the probability of Helium atoms escaping from the Moon’s surface?

Given that the mass and radius of the Moon are \(7.35\times10^{22}\,kg\) and \(1.74\times10^6\,m\) respectively, average surface temperature on the Moon is \(400\,K\), and mass of a helium atom is \(6.54\times10^{-27}\,kg\).

import numpy as np
import matplotlib.pyplot as plt

def escape(m, R, G=6.674e-11): # function for calculating escape velocity given mass and radius
    return np.sqrt((2*G*m)/R)

mM = 7.35e22 # mass of Moon (kg)
RM = 1.74e6 # radius of Moon (m) 

ve = escape(mM, RM)

print("Escape velocity of the Moon is %.f m/s" % (ve))

def find_vmean(m, T, kB=1.38e-23):
    return np.sqrt((3*kB*T)/m)

mHe = 6.54e-27 # mass of helium atom (kg)
TM = 400 # surface temperature on the Moon (T)

vm = find_vmean(mHe, TM)

print("Mean velocity of He atoms on the Moon is %.f m/s" % (vm))

def maxwell_boltzmann(v, v_mean): # maxwell-boltzmann distribution
    return v/v_mean * np.exp(-1.27*(v/v_mean)**2)

v = np.linspace(0, 5000, 1001)

prob = maxwell_boltzmann(v, vm) # array of probabilities at different velocities

# plot probability distribution

fig = plt.figure(figsize=(10,8))
plt.plot(v, prob, 'k')
plt.plot(v[475], prob[475], 'ro', label='velocity >= %.fm/s, probability = %.2f' % (v[475], prob[475]))
plt.xlabel('velocity (m/s)')
plt.ylabel('probability')
plt.title('Probability distribution of He molecules with a velocity greater than some value v', fontsize=14)
plt.legend(loc='upper right', fontsize=12)
plt.grid(True)

plt.show()

Escape velocity of the Moon is 2375 m/s
Mean velocity of He atoms on the Moon is 1591 m/s

References

Course notes from Lecture 5 of the module ESE 95011 Mechanics