Nuclides
Contents
Nuclides#
High-Temperature Geochemistry Chemistry for Geoscientists Low-Temperature Geochemistry
Atoms or nuclides consist of protons, neutrons, and electrons.
The atomic mass number of a nuclide is defined as:
A particular nuclide is completely defined with the following notation: \(^A_ZX\). e.g. \(^{118}_{50}Sn\).
\(\quad\)\(A\) = Atomic mass number = total number of nucleons = \(118\)
\(\quad\)\(Z\) = number of protons = \(50\)
\(\quad\)\(N\) = number of neutrons = \(118 - 50\) = \(68\)
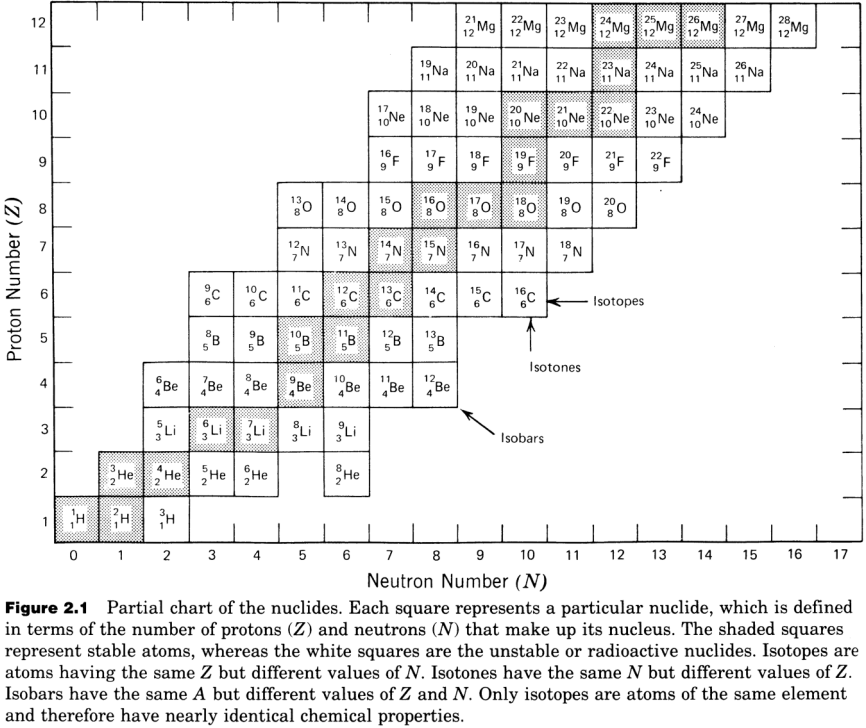
Isotopes are nuclides that have the same \(Z\) (same element) but different \(N\). They have almost identical chemical properties but different masses. For example, \(^{110}Cd\), \(^{111}Cd\), \(^{112}Cd\), \(^{113}Cd\), \(^{114}Cd\), \(^{116}Cd\).
Isobars are nuclides that have the same \(A\) (same mass number) and very similar mass, but a different combination of \(Z\) & \(N\). For example, \(^{110}Cd\) and \(^{110}Pd\), \(^{113}Cd\), \(^{113}In\).
Atomic Weight Definitions.
Atomic mass unit: \(amu\)
\(1\,amu\) = \(1/12\) of the mass of \(^{12}_6C\) = \(1.6605\times10^{-24}\,g\)
The units Dalton (\(Da\)) and amu are equivalent.
“Gram Atomic Weight” (used in chemistry) is the mass of \(1\) mole of a particular nuclide, element or molecule. For example, \(^{12}C:\,12.00\,g/mol\).
Nuclide Masses
Proton: \(1.007593\,amu\)
Neutron: \(1.008982\,amu\)
Electron: \(0.000548756\,amu\)
\(^{23}Na\): \(22.9897697\,amu\)
\(^{238}U\): \(238.050785782\,amu\)
The nuclide masses are less than sum of proton + neutron + electron masses. This mass defect is equivalent to the binding energy that holds the nucleus together:
A larger mass defect is equivalent to more binding energy and a more stable nucleus.
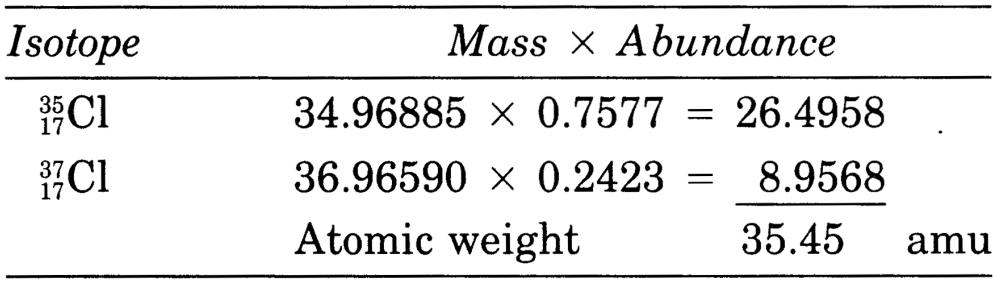
The atomic weight of an element with several isotopes is the sum of the masses of the naturally occurring isotopes, weighed in accordance of the fractional molar (not weight!) isotope abundance.
Example:
The chart of nuclides groups the isotopes in a plot of proton number \(Z\) vs. neutron number \(N\). The chart provides information on all \(264\) known stable isotopes, long-lived radioactive nuclides, and a large number of short and very short-lived radioactive nuclides. The top figure is only a small excerpt from the complete chart at the bottom!
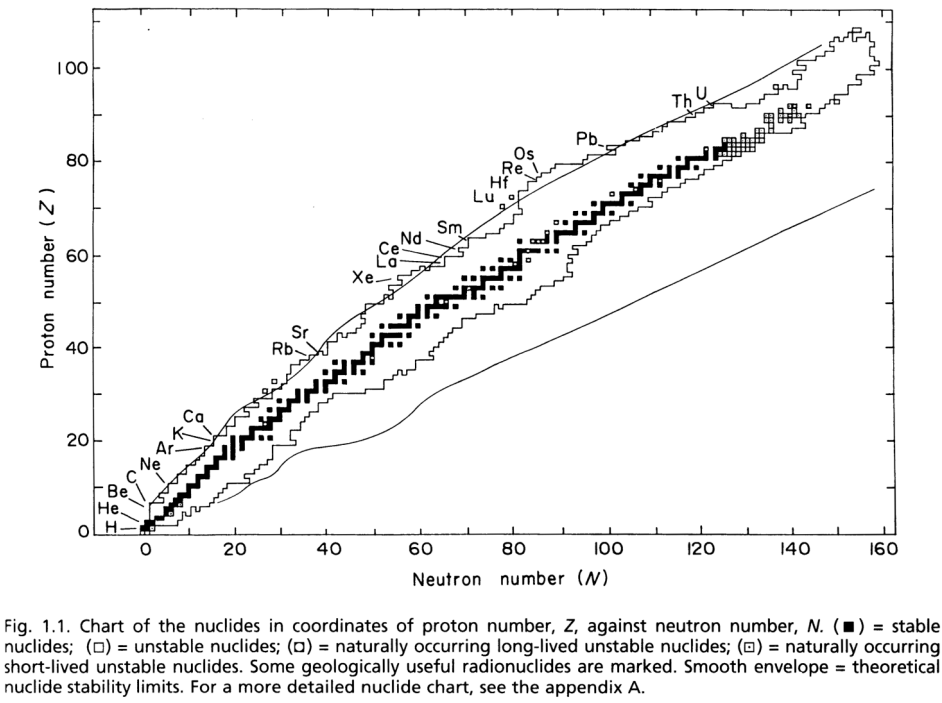
Note that:
horizontal trends are for isotopes of a single element;
diagonal downward trends are for isobars;
vertical trends are for nuclides of different elements (because \(Z\) is variable).
Stable nuclides: \(N \approx 1 \times Z\) for light elements, and \(N \approx 1.5 \times Z\) for heavy elements.
Nuclides outside of the “valley of stability” undergo transformation by radioactive decay to a stable daughter isotope.
# import relevant modules
import numpy as np
Problem Set 3#
(2) A \(100\,g\) sample of enriched uranium consists of \(62\,g\) \(^{238}U\) and \(38\,g\) \(^{235}U\).
How many moles of \(^{238}U\) and \(^{235}U\) are in the uranium sample?
How many atoms of \(^{238}U\) and \(^{235}U\) are in the uranium sample?
What is the atomic \(^{238}U/^{235}U\) ratio of the sample? How does this compare with the \(^{238}U/^{235}U\) weight ratio?
What is the atomic weight of this \(U\) sample?
Solution:
Mole can be found by the mass of a substance divided by its molar mass.
\(1\) mole of a substance is composed of an avogadro number of particles (atoms, molecules).
Atomic weight is the weighted average of all the stable isotopes.
The functions for calculating those will be developed.
# function for calculating moles from the mass a substance (g) - moles = mass / molecular weight (MW)
def g_to_mol(mass, MW):
return mass/MW
# function for calculating the number of particles from the moles a substance
def mol_to_particles(mol):
NA = 6.022 * 10**23
return mol*NA
# function for calculating the average atomic weight
def average_atomic_weight(isotopic_mass_list, proportion_list):
isotopic_mass_array = np.array(isotopic_mass_list)
proportion_array = np.array(proportion_list)
Z = np.sum(isotopic_mass_array*proportion_array/sum(proportion_list))
return Z
# print answers
g_U238 = 62
g_U235 = 38
mol_U238 = g_to_mol(g_U238, 238.0508)
mol_U235 = g_to_mol(g_U235, 235.0439)
print(f"The sample is composed of {mol_U238:.3f} mol of U-238 and {mol_U235:.3f} mol of U-235.")
atom_U238 = mol_to_particles(mol_U238)
atom_U235 = mol_to_particles(mol_U235)
print(f"The sample is composed of {atom_U238:.2e} atoms of U-238 and {atom_U235:.2e} atoms of U-235.")
print(f"The atomic U-238/U-235 ratio of the sample is {atom_U238/atom_U235:.3f}.")
print(f"The weight U-238/U-235 ratio of the sample is {g_U238/g_U235:.3f}.")
print(f"The atomic weight of this U sample is {average_atomic_weight([238.0508, 235.0439], [62, 38]):.3f} amu.")
The sample is composed of 0.260 mol of U-238 and 0.162 mol of U-235.
The sample is composed of 1.57e+23 atoms of U-238 and 9.74e+22 atoms of U-235.
The atomic U-238/U-235 ratio of the sample is 1.611.
The weight U-238/U-235 ratio of the sample is 1.632.
The atomic weight of this U sample is 236.908 amu.
(3) Calculate the number of moles of strontium in a \(1.68\,g\) sample of strontium oxide (\(SrO\)). This \(Sr\) sample is assumed to have an unusual, non-natural isotope composition with \(85\%\) \(^{84}Sr\), \(10\%\) \(^{86}Sr\), \(2\%\) \(^{87}Sr\), and \(3\%\) \(^{88}Sr\) (fractional abundances given in atomic-%).
# calculate the average atomic weight of Sr in this sample
isotopic_mass_list = [83.91343, 85.90927, 86.90889, 87.90562]
proportion_list = [85, 10, 2, 3]
MW_Sr = average_atomic_weight(isotopic_mass_list, proportion_list)
# calculate the mole of Sr in the sample, which equals the moles of SrO as SrO contains one O atom
MW_O = 15.9999
MW_SrO = MW_Sr + MW_O
g_SrO = 1.68
mol_SrO = g_to_mol(g_SrO, MW_SrO)
mol_Sr = mol_SrO
print(f"This sample contains {mol_Sr:.4f} mol of Sr.")
This sample contains 0.0168 mol of Sr.
(4) A synthetic sample of lead (\(Pb\)) has the following isotope abundances:
\(^{204}Pb:\,28\%\)
\(^{206}Pb:\,12\%\)
\(^{207}Pb:\,15\%\)
\(^{208}Pb:\,45\%\)
What is the atomic weight of the \(Pb\)? Note that this calculation is straightforward because the isotope abundances are given in atomic/molar-% (as is customary) rather than in weight-%.
# calculate the average atomic weight of Pb
isotopic_mass_list = [203.97304, 205.97446, 206.97589, 207.97604]
proportion_list = [28, 12, 15, 45]
MW_Pb = average_atomic_weight(isotopic_mass_list, proportion_list)
print(f"The atomic weight of Pb is {MW_Pb:.3f} amu.")
The atomic weight of Pb is 206.465 amu.
References#
Lecture slide and Practical for Lecture 3 of the High-Temperature Geochemistry module

