Work and Energy

Mechanics Physical Processes

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

Work-energy theorem

Mathematically, work-energy theorem is stated as the following:

\[W_{12}=\int_{x_1}^{x_2}F(x)\,dx\]

where \(W_{12}\) is the work done on a body by the force \(F\) as the body moves from point \(x_1\) to \(x_2\).

\(W_{12}\) is equal to the change in energy when the body moves from \(x_1\) to \(x_2\).

Forms of energy

Kinetic energy

\[KE=\frac{1}{2}mv^2\]

where \(m\) is mass, \(v\) is velocity

Potential energy

Gravitational potential energy

\[GPE(x)=mgx\]

where \(m\) is mass, \(g\) is gravitational acceleration, \(x\) is the height above a reference point where \(x=0\)

Elastic potential energy

\[EPE(x)=\frac{1}{2}kx^2\]

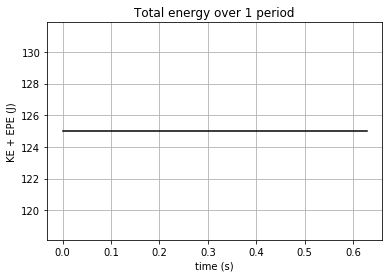
Note: total energy is constant over time

Equipartition of Energy

The principle of equipartition of energy states that at thermal equilibrium, magnitude of different forms of energy are equal on average.

Tutorial Problem 3.6

Consider a body connected to a spring, oscillating according to \(x(t)=x_0\cos(\sqrt{\frac{k}{m}}t)\).

Derive expressions for the elastic potential energy of the body as a function of time, for the kinetic energy of the body as a function of time, and for the total energy of the body as a function of time.

Draw a simple sketch of these energies as a function of time. What is the average value of \(KE\), and the average value of \(EPE\), over one period? You should find that the average values of \(KE\) and \(EPE\) are equal.

g = 9.81 # m/s2

# input arbitrary numbers
m = 10 # mass kg
k = 1e3 # spring constant N/m
x0 = 0.5 # m

T = 2 * np.pi * np.sqrt(m/k) # period in simple harmonic motion

print("Period = %.2f" % T)

t = np.linspace(0, T, 500)

X = x0 * np.cos(np.sqrt(k/m)*t)

dxdt = -x0 * np.sqrt(k/m) * np.sin(np.sqrt(k/m)*t)

epe = 0.5 * k * X**2

ke = 0.5 * m * dxdt**2

average_epe = np.sum(epe)/len(epe)

average_ke = np.sum(ke)/len(ke)

print("Average EPE = %.dJ" % (average_epe))
print("Average KE = %.dJ" % (average_ke))

# plot figures of EPE, KE, and total energy over 1 period

fig = plt.figure(figsize=(6,4))

plt.plot(t, ke+epe, 'k')
plt.xlabel('time (s)')
plt.ylabel('KE + EPE (J)')
plt.title('Total energy over 1 period')
plt.grid(True)

plt.show()

Period = 0.63
Average EPE = 62J
Average KE = 62J

nframes = len(t)

# Plot background axes
fig, axes = plt.subplots(1,3, figsize=(15, 10))

line1, = axes[0].plot([], [], 'ko', lw=2)
line2, = axes[1].plot([], [], 'ro', lw=2)
line3, = axes[2].plot([], [], 'bo', lw=2)


axes[0].set_xlim(-0.1, 0.1)
axes[0].set_ylim(-0.6, 0.6)
axes[0].set_ylabel('displacement (m)')
axes[0].set_title('Motion of body over 1 period')
axes[1].set_xlim(-0.1, 0.1)
axes[1].set_ylim(0, 130)
axes[1].set_ylabel('EPE (J)')
axes[1].set_title('Elastic potential energy over 1 period')
axes[2].set_xlim(-0.1, 0.1)
axes[2].set_ylim(0, 130)
axes[2].set_ylabel('KE (J)')
axes[2].set_title('Kinetic energy over 1 period')
    
lines = [line1, line2, line3]

# Plot background for each frame
def init():
    for line in lines:
        line.set_data([], [])
    return lines

# Set what data to plot in each frame
def animate(i):
    
    x1 = 0
    y1 = X[i]
    lines[0].set_data(x1, y1)
    
    x2 = 0
    y2 = epe[i]
    lines[1].set_data(x2, y2)
    
    x3 = 0
    y3 = ke[i]
    lines[2].set_data(x3, y3)
    
    return lines

# Call the animator
anim = animation.FuncAnimation(fig, animate, init_func=init,
                               frames=nframes, interval=10, blit=True)

HTML(anim.to_html5_video())

References

Course notes from Lecture 3 of the module ESE 95011 Mechanics