Sm-Nd Decay
Contents
Sm-Nd Decay#
# import relevant modules
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from IPython.display import display
from math import log10, floor
# create our own functions
# function to round a value to a certain number of significant figures
def round_to_n_sf(value, no_of_significant_figures):
value_rounded = round(value, no_of_significant_figures-1-int(floor(log10(abs(value)))))
if value_rounded == int(value_rounded):
value_rounded = int(value_rounded)
return value_rounded
Sm-Nd Decay System#
Both \(Sm\) (samarium) and \(Nd\) (neodymium) are Rare Earth Elements (\(REEs\)). In nature, both elements generally occur in dispersed form, with typical concentrations in mantle and crustal rocks of less than \(\sim20\,ppm\).
Most \(REEs\), including \(Sm\) and \(Nd\), occur as trivalent (\(3+\)) ions with ionic radii that decrease systematically with increasing atomic number, so \(Sm\) has a smaller ionic radius than \(Nd\).
Both \(Nd\) and \(Sm\) are moderately incompatible elements, but \(Nd\) is slightly more incompatible than \(Sm\) during mantle melting because it has a slightly larger ionic radius.
The \(REEs\) are generally considered to be relatively resistant toward mobilization by fluids – they are fluid-immobile elements.
Dating of Terrestrial Rocks#
The continental crust in general and siliceous rocks in particular have low and relatively uniform \(Sm/Nd\) ratios (= parent/daughter ratio), so the \(Sm\)-\(Nd\) system is not particularly suitable for dating such rocks. On the other hand, mafic and ultramafic rocks have variable and high \(Sm/Nd\) ratios, so they are good candidates for \(Sm\)-\(Nd\) dating.
Due to the fluid immobility of the \(REEs\), \(Sm\)-\(Nd\) ages and initial \(Nd\) isotope compositions are not very sensitive to weathering and metamorphism.
Notice how the \(Sm\)-\(Nd\) system is opposite to the \(Rb\)-\(Sr\) decay system in many ways!
# Sm-Nd decay equation - very similar to the Rb-Sr one
# each return depends on what we want to find from the equation
def Sm_Nd_decay_equation(Nd143_Nd144_ratio, initial_Nd143_Nd144_ratio, Sm147_Nd144_ratio, t):
decay_const_Sm = 6.54 * 10**-12 # yr^-1 # decay constant of Sm-147
if Nd143_Nd144_ratio == '?':
return initial_Nd143_Nd144_ratio + Sm147_Nd144_ratio*(np.exp(decay_const_Sm*t)-1)
elif initial_Nd143_Nd144_ratio == '?':
return Nd143_Nd144_ratio - Sm147_Nd144_ratio*(np.exp(decay_const_Sm*t)-1)
elif Sm147_Nd144_ratio == '?':
return (Nd143_Nd144_ratio - initial_Nd143_Nd144_ratio)/(np.exp(decay_const_Sm*t)-1)
Problem Set 5#
Question 1#
A pigeonite basalt (\(12039\), \(19\)) from the Moon yielded the following results:
# create a dataframe to show the obtained results
samples = ["Whole rock", "Plagioclase", "Pyroxene"]
Sm147_Nd144_ratio = [0.2090, 0.1727, 0.2434]
Nd143_Nd144_ratio = [0.513142, 0.512365, 0.513861]
dict1 = {'Samples' : samples,
'$${^{147}Sm}/{^{144}Nd}$$' : Sm147_Nd144_ratio,
'$${^{143}Nd}/{^{144}Nd}$$' : Nd143_Nd144_ratio}
df1 = pd.DataFrame(dict1)
df1.loc[:, '$${^{147}Sm}/{^{144}Nd}$$'] = df1['$${^{147}Sm}/{^{144}Nd}$$'].map('{:g}'.format)
df1.loc[:, '$${^{143}Nd}/{^{144}Nd}$$'] = df1['$${^{143}Nd}/{^{144}Nd}$$'].map('{:g}'.format)
display(df1.style.hide_index())
| Samples | $${^{147}Sm}/{^{144}Nd}$$ | $${^{143}Nd}/{^{144}Nd}$$ |
|---|---|---|
| Whole rock | 0.209 | 0.513142 |
| Plagioclase | 0.1727 | 0.512365 |
| Pyroxene | 0.2434 | 0.513861 |
a) Plot the data in an isochron diagram. Scale the y-axis from about \({^{143}Nd}/{^{144}Nd}\) = \(0.5080\) to \(0.5150\) and the x-axis from \({^{147}Sm}/{^{144}Nd}\) = \(0\) to about \(0.3\).
b) Determine the age and initial \({^{143}Nd}/{^{144}Nd}\) ratio of this rock from the slope and y-intercept of the isochron.
c) Calculate the \(Nd\) isotope ratio of CHUR for the age of rock.
d) Express the initial \(Nd\) isotope composition of the rock as an \(\epsilon_{Nd}\) value relative to \(CHUR\). What does the initial \(\epsilon_{Nd}\) value tell you, if you assume that the Moon as a whole has chondritic \(Sm/Nd\) and \(Nd\) isotope ratios?
Solution:
a) See below
# Question 1a
# set figure size
plt.figure(figsize=(8,6))
# Plot data points
plt.plot(Sm147_Nd144_ratio, Nd143_Nd144_ratio, 'ro', label="Data points")
# plot isochron by fitting a polynomial degree 1 - ie a straight line.
poly_coeffs=np.polyfit(Sm147_Nd144_ratio, Nd143_Nd144_ratio, 1)
p1 = np.poly1d(poly_coeffs)
slope = poly_coeffs[0] # e^(\lambda t) - 1
y_intercept = poly_coeffs[1] # initial Nd143/Nd144 ratio
x = np.linspace(0, 0.3, 10) # Sm147/Nd144 ratio
plt.plot(x, p1(x), 'b', label="linear fit ($y = %gx + %g$)" % (round_to_n_sf(slope, 3), round_to_n_sf(y_intercept, 3)))
# label and title the plot
plt.xlabel('${^{147}Sm}/{^{144}Nd}$')
plt.ylabel('${^{143}Nd}/{^{144}Nd}$')
plt.title('Isochron plot', fontsize=14)
plt.legend(loc='best', fontsize=10)
<matplotlib.legend.Legend at 0x1f58e092ca0>
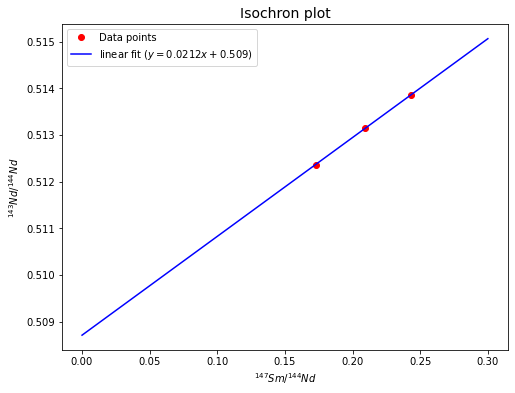
b) Now we have already got the slope (\(m\)) and y-intercept (\(b\)) of the isochron, so we can estimate the age (\(t\)) and initial \(Nd\)-\(143/Nd\)-\(144\) ratio (\(({^{143}Nd}/{^{144}Nd})_0\)) since
# Question 1b
decay_const_Sm = 6.54 * 10**-12 # yr^-1 # decay constant of Sm-147
t = (1/decay_const_Sm) * np.log(slope + 1) # age
b = y_intercept # initial Nd143/Nd144 ratio
# print answers
print("The age implied by the isochron is %.2e yr." % t)
print("The initial Nd-143/Nd-144 ratio is %.6f." % b)
The age implied by the isochron is 3.20e+09 yr.
The initial Nd-143/Nd-144 ratio is 0.508713.
As the distribution and evolution of \(Sm\) and \(Nd\) in the Earth are not explained in this page where we focus on quantitative parts, we will recall the concepts of CHUR and \(\epsilon_{Nd}\) from the lecture slide before attempting questions c and d.
CHUR (Chondritic Uniform Reservoir) is defined by the average present-day \(Sm/Nd\) ratio and \(Nd\) isotope composition of chondritic meteorites. It is representative for the \(Nd\) isotope composition and evolution of the bulk Earth and bulk silicate Earth. The present-day \(Nd\) isotope composition of chondrites is \(({^{143}Nd}/{^{144}Nd})_{CHUR} = 0.512638\). The average \(({^{147}Sm}/{^{144}Nd})_{CHUR} = 0.1967\).
It is convenient to consider past and present variations in \(Nd\) isotope compositions relative to the isotopic evolution of CHUR. This is done using the \(\epsilon\) notation:
\(\epsilon_{Nd}\) values denote relative differences in \(Nd\) isotope compositions (relative to CHUR) in parts per \(10,000\).
c) From b), the age of the basalt is \(3.20\,Gyr\). So, in this question, we are going to calculate \(({^{143}Nd}/{^{144}Nd})_{CHUR}\) at \(3.20\,Gya\) using the \(Sm\)-\(Nd\) decay equation (very similar to \(Rb\)-\(Sr\) decay equation):
In this case:
\(\quad {^{143}Nd}/{^{144}Nd} = ({^{143}Nd}/{^{144}Nd})_{CHUR,\,present} = 0.512638\)
\(\quad ({^{143}Nd}/{^{144}Nd})_0 = ({^{143}Nd}/{^{144}Nd})_{CHUR,\,3.20\,Gyr} =\) haven’t know yet
\(\quad {^{147}Sm}/{^{144}Nd} = ({^{147}Sm}/{^{144}Nd})_{CHUR,\,present} = 0.1967\)
\(\quad \lambda = 6.54 \times 10^{-12}\,yr^{-1}\)
\(\quad t = 3.20 \times 10^9\,yr\)
# Question 1c
# Given values
Nd143_Nd144_ratio = 0.512638
Sm147_Nd144_ratio = 0.1967
t = 3.2 * 10**9 # yr
initial_Nd_ratio_CHUR = Sm_Nd_decay_equation(Nd143_Nd144_ratio, '?', Sm147_Nd144_ratio, t) # Nd isotope ratio of CHUR at 3.20 Gya
# print answer
print("The Nd isotope ratio of CHUR at 3.20 Gya is %g." % round_to_n_sf(initial_Nd_ratio_CHUR, 6))
The Nd isotope ratio of CHUR at 3.20 Gya is 0.508478.
d)
From b), the initial \(Nd\) isotope ratio of the rock is \(0.508713\).
From c), the initial \(Nd\) isotope ratio of CHUR is \(0.508478\).
Calculate the initial value of \(\epsilon_{Nd}\) (at \(t = 3.20\,Gyr\))
# function to calculate epsilon Nd
def epsilon_Nd(Nd_ratio_rock, Nd_ratio_CHUR):
return (Nd_ratio_rock - Nd_ratio_CHUR)/Nd_ratio_CHUR * 10000
# Question 1d
# Given values
initial_Nd_ratio_rock = 0.508713
initial_Nd_ratio_CHUR = 0.508478
# print answer
print("The initial differences in Nd isotope compositions (relative to CHUR) of the rock in parts per 10,000 is %g." \
% round_to_n_sf(epsilon_Nd(initial_Nd_ratio_rock, initial_Nd_ratio_CHUR), 3))
The initial differences in Nd isotope compositions (relative to CHUR) of the rock in parts per 10,000 is 4.62.
The positive \(\epsilon_{Nd}\) initial value means that the rock comes from a depleted source. The depleted source is probably the lunar mantle, which was depleted by the formation of the lunar crust.
Question 2#
Neodymium model ages or crustal residence ages are obtained by calculating the intersection of the \(Nd\) isotope evolution of a rock sample with the \(Nd\) isotope evolution of a reservoir (RES) that is assumed to have a composition akin to CHUR (for \(t_{CHUR}\)) or a depleted mantle (DM) composition (for \(t_{DM}\)).
The respective Nd isotope evolutions evolution curves are given by:
Sample:
CHUR or DM reservoir:
The intersections is obtained by equating \(\left(\frac{^{143}Nd}{^{144}Nd}\right)_{Sam,0} = \left(\frac{^{143}Nd}{^{144}Nd}\right)_{Res,0}\)
After rearranging this yields for \(t\):
Calculate the \(t_{DM}\) for a sample characterized by \({^{147}Sm}/{^{144}Nd} = 0.102\) and \({^{143}Nd}/{^{144}Nd} = 0.511552\). The depleted mantle is assumed be characterized by \({^{147}Sm}/{^{144}Nd} = 0.222\) and \({^{143}Nd}/{^{144}Nd} = 0.513114\).
# Question 2
# decay constant of Sm-147
decay_const = 6.54 * 10**-12 # yr^-1
# isotopic ratios of the sample
Sm147_Nd144_ratio_sample = 0.102
Nd143_Nd144_ratio_sample = 0.511552
# isotopic ratios of the depleted mantle
Sm147_Nd144_ratio_DM = 0.222
Nd143_Nd144_ratio_DM = 0.513114
# calculate t
t = (1/decay_const) * np.log(((Nd143_Nd144_ratio_sample - Nd143_Nd144_ratio_DM)/(Sm147_Nd144_ratio_sample - Sm147_Nd144_ratio_DM)) + 1)
# print answer
print("The Nd model age is %.2e yrs." % t)
The Nd model age is 1.98e+09 yrs.
References#
Lecture slide and Practical for Lecture 5 of the High-Temperature Geochemistry module

