Attenuation

Waves

In this notebook, the different types of attenuation will be discussed. Group velocity and dispersion are discussed here (link?).

Attenuation is the loss of intensity as waves travel through a medium.

import numpy as np
import matplotlib.pyplot as plt

1. Dispersion

In dispersion, higher frequency waves travel faster than lower frequency waves. The energy spreads out thus leaving less intensity for the pulses.

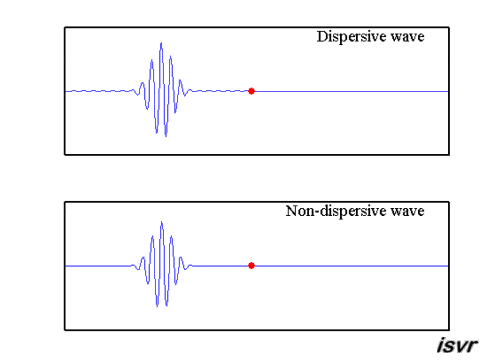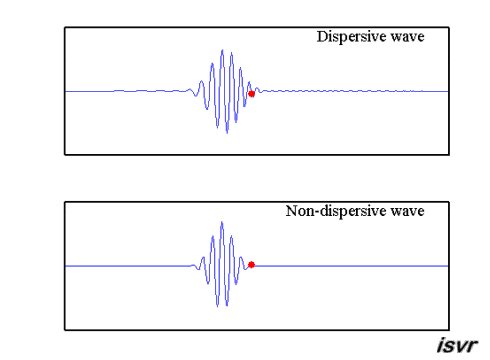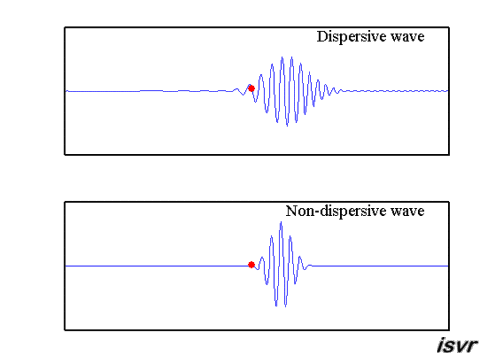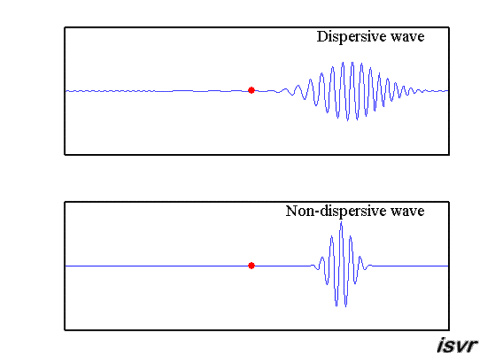
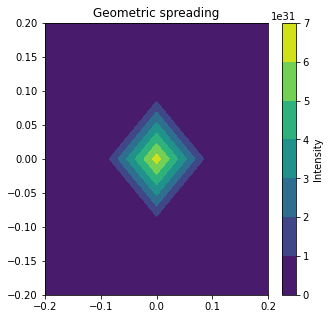
2. Geometric spreading

Energy spreads out as a function of area. Thus, intensity decreases away from the source. It is important to look at the dimensions of spreading, i.e. water waves pread in 2D so the area is \(2\pi r\). Body waves spread out in 3D, so the area to consider is \(2 \pi r^2\). Geometric spreading is defined as initial intensity divided by the area as a function of distance from the source so

\[\frac{I_0}{area}\]

For example, \(\frac{I_0}{2\pi r}\) for water waves.

x = np.arange(-0.5,0.5,0.1)
y = np.arange(-0.5,0.5,0.1)
X, Y = np.meshgrid(x,y)

I_0 = 10
r = (X**2+Y**2)**0.5 # calculate radius
z = I_0/(2 * np.pi * r**2) # geometric spreading 
fig, ax= plt.subplots(figsize = (5,5))
CS = plt.contourf(X,Y,z)
plt.xlim(-0.2, 0.2)
plt.ylim(-0.2, 0.2)
cbar = plt.colorbar()
cbar.set_label('Intensity', rotation=90)
plt.title('Geometric spreading')
plt.show()

3. Scattering

Scattering occurs when a medium’s impedance has length scales that are smaller than the wavelength of the wave. These changes can also cause reflection and transmission.

4. Intrinsic attenuation

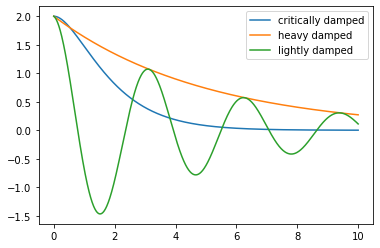
Gradual loss of energy from the wave, due to materials not being perfectly elastic. This energy is converted into heat. Attenuation can cause damping of particle motion. If there is a friction that opposes the motion of oscillation, the equation of motion for the particle becomes

\[m \frac{d^2 y}{d t^2} = -sy -r \frac{dy}{dt}\]

This equation has three solutions:

• Heavy damping: strongest case of attenuation, prohibiting the particle to oscillate. Solution of the form \(y=Ce^{-at}\). So damping in this situation is stronger than the restoring force.

• Critical damping: solution of the form \(y=(A+Bt)e^{-pt}\). Less attenuation than in heavy damping case, but returns to rest position more quickly still if it has zero velocity at the start.

• Light damping is of the form \(y=y_0e^{-bt}\cos(\omega t + \phi)\).

t = np.linspace(0,10,1001)
a = 2
w = 2
damping_factor = (1+1*t)*np.exp(-t)
y = damping_factor * a 
plt.plot(t,y, label = 'critically damped')

damping_factor2 = np.exp(-0.2*x)
y2 = damping_factor2 * a 
plt.plot(x,y2, label = 'heavy damped')

damping_factor3 = np.exp(-0.2*x)
y2 = damping_factor2 * a * np.cos(w * x)
plt.plot(x,y2, label = 'lightly damped')
# plt.legend()

plt.legend()
plt.show()

Quality factor

The quality factor is of the form

\[ Q = \frac{m \omega_0}{r}\]

where \(\omega_0 =\sqrt{\frac{s}{m}}\), the natural frequency.