Holomorphic functions

Complex differentiation

Holomorphic functions (often called complex analytic functions)

A function \(f : D \to \mathbb{C}\), where \(D \subseteq \mathbb{C}\) is an open set, is complex-differentiable at a point \(z_0 \in D\) if there exists

\[ f'(z_0) = \lim_{z \to z_0} \frac{f(z) - f(z_0)}{z - z_0} \in \mathbb{C}. \]

If \(f : D \to \mathbb{C}\) is differentiable at all points of \(D\), we say it is holomorphic (often analytic) in \(D\). If a function is holomorphic in \(\mathbb{C}\) we say that it is entire.

Examples:

• \(z\) is entire

• all polynomials are entire

• \( 1/z \) is holomorphic in \( \mathbb{C} \backslash \{ 0 \} \)

• all rational functions are holomorphic in \(\mathbb{C}\) except in the zeros of their denominators

• \( \sin z, \cos z \) are entire

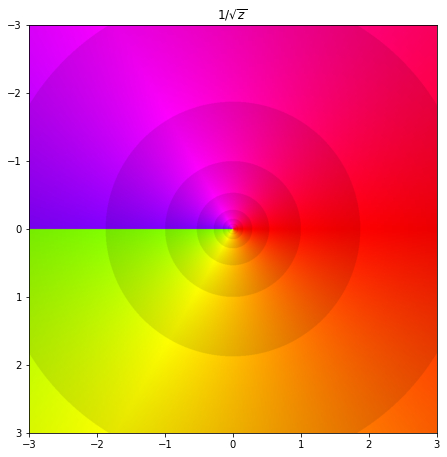
• \( \sqrt{z} \) is holomorphic in \(\mathbb{C} \backslash (- \infty, 0]\)

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import hsv_to_rgb


def phaseplot(ax, f, x=None, y=None):

    a = np.log(np.abs(f)) * 20 / (2*np.pi)
    a = a - a//1
    _amin = np.min(a)
    _amax = np.max(a)
    
    h = (np.angle(-f) + np.pi) / (2*np.pi)
    v = (a - _amin) / (_amax - _amin) * (1 - 0.9) + 0.9
    
    if x is None:
        extent = None
    else:
        extent = [min(x), max(x), min(y), max(y)]
    
    img = hsv_to_rgb(np.dstack((h, np.ones(f.shape), v)))
    
    ax.imshow(img, extent=extent)
    ax.invert_yaxis()
    
    
x = np.linspace(-3, 3, 1000)
X, Y = np.meshgrid(x, x)
Z = X + 1j*Y

fig = plt.figure(figsize=(7.5, 7.5))
ax = fig.add_subplot()
ax.set_title('$1/ \sqrt{z}$')

phaseplot(ax, 1/np.sqrt(Z), x, x)
plt.show()

If we go back to thinking about a derivative of a real function of one variable, recall that for the derivative to exist at \(x_0\) the limit when approaching \(x_0\) from the left and from the right must be equal to each other. That is because \(x_0\) is just a number on the number line. Complex numbers, however, lie on the plane, so we can approach some complex number \(z_0\) from any direction. Therefore, the limit above must exist for any angle of approach to \(z_0\) and it must always be the same. This is a very strict condition!

For \(f\) to be differentiable at \(z_0\) it must be continuous at \(z_0\). That means that

\[ \lim_{z \to z_0} f(z) = f(z_0) \]

for finite \(z_0, f(z_0)\). Recall that we can separate the real and imaginary parts of a complex function: \(f(z) = u(x, y) + iv(x, y)\). For \(f\) to be continuous, it is enough to show that \(u\) and \(v\) are continuous. If \(f\) is holomorphic on \(D\) then it is continuous on \(D\).

Differentiation rules

The addition, product, quotient and chain rules apply in complex differentiation similarly to real calculus. Let \(f, g : D \to \mathbb{C}\) be differentiable at \(z_0 \in D\), then:

• \(\alpha f + \beta g\) is differentiable for all \( \alpha, \beta \in \mathbb{C} \) at \(z_0\): \( (\alpha f + \beta g)'(z_0) = \alpha f' (z_0) + \beta g'(z_0) \)

• \(fg\) is differentiable at \(z_0\): \((fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_o)\)

• \(\frac{f}{g}\) is differentiable at \(z_0\) for \(g(z_0) \neq 0\): \( \left( \frac{f}{g} \right)' (z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{(g(z_0))^2} \)

• Let \(h: D_1 \to \mathbb{C}\), where \(D_1\) is an open set containing \(f(D)\). If \(h\) is differentiable at \(f(z_0)\), then \(h \circ f\) is differentiable at \(z_0\): \( (h \circ f)'(z_0) = h'(f(z_0))f'(z_0). \)

Cauchy-Riemann conditions

Cauchy-Riemann theorem. A complex function \(f = u + iv : D \to \mathbb{C}\) is differentiable at a point \(z_0 = (x_0, y_0)\) iff the real-valued functions of two real variables \(u\) and \(v\) are differentiable at a point \((x_0, y_0)\) and they satisfy the Cauchy-Riemann conditions:

\[ \partial_x u = \partial_y v, \qquad \partial_y u = - \partial_x v. \]

This is a fundamental result in complex analysis - a necessary and sufficient condition for any complex function to be differentiable. Furthermore,

\[\begin{split} \begin{aligned} f'(z_0) & = \partial_x u + i \partial_x v =: \partial_x f(z_0) \\ & = \partial_x u - i \partial_y u \\ & = \partial_y v - i \partial_y u =: -i \partial_y f(z_0) = \frac{1}{i} \partial_y f(z_0) = \partial_{iy} f(z_0) \\ & = \partial_y v + i \partial_x v. \end{aligned} \end{split}\]

If Cauchy-Riemann conditions are satisfied, then \(u\) and \(v\) are harmonic functions, i..e they are a solution to the Laplace equation:

\[ u_{xx} + u_{yy} = 0. \]

Examples: basic derivatives

\[ (z^n)' = nz^{n-1} \]

\[\begin{split} \begin{aligned} \exp' z & = (e^x(\cos y + i \sin y))' \\ & = \partial_x u(z) + i \partial_x v(z) = \partial_x (e^x \cos y) + i \partial_x (e^x \sin y) = e^x \cos y + i e^x \sin y \\ & = \exp z \end{aligned}\end{split}\]