Hess’ law
Contents
Hess’ law#
Low-Temperature Geochemistry Chemistry for Geoscientists
Hess’ law states that the total enthalpy change between reactants and products is independent of the route taken, e.g. if \(X\) is converted to \(Y\) and then \(Y\) to \(Z\), the total enthalpy change will be the same as if \(X\) was converted directly to \(Z\) (see the figure below).
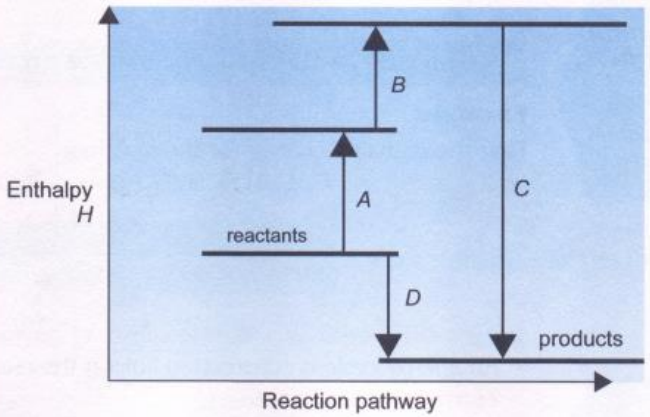
The standard enthalpy change for a chemical reaction is equal to the sum of the standard molar enthalpies of formation of all the products, each one multiplied by the number of moles of the product in the balanced chemical equation, minus the corresponding sum for the reactants.
where \(v_i\) are stoichiometric coefficients (how many moles of stuff).
Hess’ law applicable to any state function: \(U, S, \bar{V}, H, A, G, C_P, C_V\).
In this session, a function called “Hess_law_calculator” was developed to calculate a thermodynamic quantity for a given reaction.
# import relevant modules
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from IPython.display import display
# Hess' law calculator - return a quantity (e.g. enthalpy, entropy, Gibbs' free energy) of a given reaction
# 'reaction' is a string of latex-style chemical equation with certain syntax - no space
def hess_law_calculator(reaction, quantity_dict):
# remove space, '$', and state labels
reaction = reaction.replace(' ', '').replace("$", '').replace("(s)", '').replace("(l)", '').replace("(g)", '').replace("(aq)", '')
# check where is the '=' symbol, and split into 2 strings
half_reactions = reaction.split('=')
# check where is the '+' symbol between components, change it to '/' and split each component by it
# reactants
reactants = half_reactions[0]
r = ''
for i in range(len(reactants)-1):
if reactants[i] == '+' and reactants[i+1] not in '=+}' :
r += '/'
else:
r += reactants[i]
r += reactants[-1] # last character
reactants_with_coeff = r.split('/')
# products
products = half_reactions[1]
p = ''
for i in range(len(products)-1):
if products[i] == '+' and products[i+1] not in '=+}' :
p += '/'
else:
p += products[i]
p += products[-1] # last character
products_with_coeff = p.split('/')
species_with_coeff = reactants_with_coeff + products_with_coeff
# extract stoichiometric coefficients and remove coefficients from species
coeff_list = []
species_without_coeff = []
for s in species_with_coeff:
coeff_str = ''
for i in range(len(s)):
if s[i] in "1234567890.":
coeff_str += s[i]
else:
if coeff_str == '':
coeff_str = '1'
coeff_float = float(coeff_str)
if s in reactants_with_coeff:
coeff_float = -coeff_float
coeff_list.append(coeff_float)
species_without_coeff.append(s[i:len(s)])
break
# calculate thermodynamic quantity of the given reaction using Hess' law
total_quantity = 0
for i in range(len(species_without_coeff)):
if species_without_coeff[i] in quantity_dict.keys():
total_quantity += quantity_dict[species_without_coeff[i]] * coeff_list[i]
return total_quantity
Lesson 2 - Problem 3 (Using thermodynamic data)#
Using the data provided in the table below, find the standard enthalpy changes and free energy changes for the following reactions (under standard conditions – beware of units in that table!):
\(\quad\)(i) \(Sn + O_2 = SnO_2\)
\(\quad\)(ii) \(KCl(s) = K^+(aq) + Cl^-(aq)\)
\(\quad\)(iii) \(2FeCO_3 + 0.5O_2 + 2H_2O = Fe_2O_3 + 2H_2CO_3\)
\(\quad\)(iv) Which of these reactions proceed spontaneously in the forward direction (i.e. from left to right, as written)?
\(\quad\)(v) Which compound is more stable in contact with air at standard temperature:
\(\qquad\)- Tin (\(Sn\)) or cassiterite (tin oxide: \(SnO_2\))?
\(\qquad\)- Hematite (\(Fe_2O_3\)) or siderite (\(FeCO_3\))?
Note: In the table below, the values of \(\Delta H\) are given in the standard units of \(kJ\,mol^{-1}\). The units of \(\Delta S^o\) are also in standard form, but for entropy, that is \(J\,mol^{-1}K^{-1}\). This difference in units must be considered if calculating \(\Delta G_T\) using \(\Delta G_T = \Delta H - T \Delta S\). That latter equation can be used to approximate a value for \(\Delta G_T\) at other temperature than standard conditions (this is an approximation though!).
# The thermodynamic data
species = ['Sn', 'O_2', 'SnO_2', 'KCl', 'K^+', 'Cl^-', 'FeCO_3', 'H_2O', 'Fe_2O_3', 'H_2CO_3']
species_for_print = ["$$"+s+"$$" for s in species]
delta_G_data_1 = [0, 0, -519.6, -409.1, -283.3, -131.3, -666.7, -237.1, -742.2, -623.1]
delta_H_data_1 = [0, 0, -580.7, -436.7, -252.4, -167.2, -740.6, -285.8, -824.2, -699.7]
delta_S_data_1 = [51.6, 205.1, 52.3, 82.6, 102.5, 56.5, 92.9, 69.9, 87.4, 187.4]
# create a dataframe
dict1 = {
'Formula' : species_for_print,
'$$\Delta G^o\,(kJ\,mol^{-1})$$' : delta_G_data_1,
'$$\Delta H^o\,(kJ\,mol^{-1})$$' : delta_H_data_1,
'$$S^o\,(J\,mol^{-1}K^{-1})$$' : delta_S_data_1,
}
df1 = pd.DataFrame(dict1)
df1.loc[:, '$$\Delta H^o\,(kJ\,mol^{-1})$$'] = df1['$$\Delta H^o\,(kJ\,mol^{-1})$$'].map('{:.1f}'.format)
df1.loc[:, '$$S^o\,(J\,mol^{-1}K^{-1})$$'] = df1['$$S^o\,(J\,mol^{-1}K^{-1})$$'].map('{:.1f}'.format)
display(df1.style.hide_index())
| Formula | $$\Delta G^o\,(kJ\,mol^{-1})$$ | $$\Delta H^o\,(kJ\,mol^{-1})$$ | $$S^o\,(J\,mol^{-1}K^{-1})$$ |
|---|---|---|---|
| $$Sn$$ | 0.0 | 0.0 | 51.6 |
| $$O_2$$ | 0.0 | 0.0 | 205.1 |
| $$SnO_2$$ | -519.6 | -580.7 | 52.3 |
| $$KCl$$ | -409.1 | -436.7 | 82.6 |
| $$K^+$$ | -283.3 | -252.4 | 102.5 |
| $$Cl^-$$ | -131.3 | -167.2 | 56.5 |
| $$FeCO_3$$ | -666.7 | -740.6 | 92.9 |
| $$H_2O$$ | -237.1 | -285.8 | 69.9 |
| $$Fe_2O_3$$ | -742.2 | -824.2 | 87.4 |
| $$H_2CO_3$$ | -623.1 | -699.7 | 187.4 |
We need to calculate the Gibbs free energy change of a reaction (\(\Delta G_r\)) in order to know if the reaction proceeds spontaneously in the forward direction. We already have \(\Delta G\) of each species, so we can find \(\Delta G_r\) directly by Hess’ law. Alternatively, we can use Hess’ law to calculate the enthalpy and entropy changes of the reaction (\(\Delta H_r, \Delta S_r\)), and then use the formula \(\Delta G_T = \Delta H - T \Delta S\).
# reactions
rxn_i = "$Sn + O_2 = SnO_2$"
rxn_ii = "$KCl(s) = K^+(aq) + Cl^-(aq)$"
rxn_iii = "$2FeCO_3 + 0.5O_2 + 2H_2O = Fe_2O_3 + 2H_2CO_3$"
# calculate the enthalpy, entropy, and gibbs free energy changes of each of the reactions
dH_r_i = hess_law_calculator(rxn_i, dict(zip(species, delta_H_data_1)))
dH_r_ii = hess_law_calculator(rxn_ii, dict(zip(species, delta_H_data_1)))
dH_r_iii = hess_law_calculator(rxn_iii, dict(zip(species, delta_H_data_1)))
dS_r_i = hess_law_calculator(rxn_i, dict(zip(species, delta_S_data_1)))
dS_r_ii = hess_law_calculator(rxn_ii, dict(zip(species, delta_S_data_1)))
dS_r_iii = hess_law_calculator(rxn_iii, dict(zip(species, delta_S_data_1)))
dG_r_i = hess_law_calculator(rxn_i, dict(zip(species, delta_G_data_1)))
dG_r_ii = hess_law_calculator(rxn_ii, dict(zip(species, delta_G_data_1)))
dG_r_iii = hess_law_calculator(rxn_iii, dict(zip(species, delta_G_data_1)))
# check if the reaction proceeds spontaneously in the forward reaction
def spontaneity_checker(dG):
if dG > 0: return "∆G > 0, so the forward reaction is non-spontaneous."
elif dG == 0: return "∆G = 0, so the reaction is in equilibrium."
else: return "∆G < 0, so the forward reaction is spontaneous."
# print the answers
print(
"(i)\n\
The enthalpy change of the reaction is %.1f kJ.\n\
The entropy change of the reaction is %.1f J/K.\n\
By Hess' law, the Gibbs free energy change of the reaction is %.1f kJ.\n\
Alternatively, since ∆G = ∆H − T∆S, the Gibbs free energy change of the reaction is %.1f kJ.\n\
%s"
% (dH_r_i, dS_r_i, dG_r_i, dH_r_i - (298.15*dS_r_i/1000), spontaneity_checker(dG_r_i)))
print(
"(ii)\n\
The enthalpy change of the reaction is %.1f kJ.\n\
The entropy change of the reaction is %.1f J/K.\n\
By Hess' law, the Gibbs free energy change of the reaction is %.1f kJ.\n\
Alternatively, since ∆G = ∆H − T∆S, the Gibbs free energy change of the reaction is %.1f kJ.\n\
%s"
% (dH_r_ii, dS_r_ii, dG_r_ii, dH_r_ii - (298.15*dS_r_ii/1000), spontaneity_checker(dG_r_ii)))
print(
"(iii)\n\
The enthalpy change of the reaction is %.1f kJ.\n\
The entropy change of the reaction is %.1f J/K.\n\
By Hess' law, the Gibbs free energy change of the reaction is %.1f kJ.\n\
Alternatively, since ∆G = ∆H − T∆S, the Gibbs free energy change of the reaction is %.1f kJ.\n\
%s"
% (dH_r_iii, dS_r_iii, dG_r_iii, dH_r_iii - (298.15*dS_r_iii/1000), spontaneity_checker(dG_r_iii)))
(i)
The enthalpy change of the reaction is -580.7 kJ.
The entropy change of the reaction is -204.4 J/K.
By Hess' law, the Gibbs free energy change of the reaction is -519.6 kJ.
Alternatively, since ∆G = ∆H − T∆S, the Gibbs free energy change of the reaction is -519.8 kJ.
∆G < 0, so the forward reaction is spontaneous.
(ii)
The enthalpy change of the reaction is 17.1 kJ.
The entropy change of the reaction is 76.4 J/K.
By Hess' law, the Gibbs free energy change of the reaction is -5.5 kJ.
Alternatively, since ∆G = ∆H − T∆S, the Gibbs free energy change of the reaction is -5.7 kJ.
∆G < 0, so the forward reaction is spontaneous.
(iii)
The enthalpy change of the reaction is -170.8 kJ.
The entropy change of the reaction is 34.1 J/K.
By Hess' law, the Gibbs free energy change of the reaction is -180.8 kJ.
Alternatively, since ∆G = ∆H − T∆S, the Gibbs free energy change of the reaction is -181.0 kJ.
∆G < 0, so the forward reaction is spontaneous.
A negative \(\Delta G\) indicates that this reaction proceeds spontaneously in the forward direction, i.e
native tin oxidises to cassiterite on exposure to air – the oxide is more stable
siderite oxidises to hematite on exposure to air and water – hematite is more stable
Lesson 2 - Problem 4 (Using Gibbs free energy to predict equilibrium)#
Using the data from White (2013),
(i) Calculate \(\Delta G_r\) for the following reaction at \(298\,K\) and \(1\,bar\):
(ii) Which of mineral assemblage (anorthite + 2 forsterite) or (diopside + spinel + 2 enstatite) is more stable under these conditions?
# The thermodynamic data
species = ['CaAl_2Si_2O_8', 'Mg_2SiO_4', 'CaMgSi_2O_6', 'MgAl_2O_4', 'MgSiO_3']
species_for_print = ["$$"+s+"$$" for s in species]
delta_G_data_2 = [-3991.86, -2056.70, -3029.22, -2163.15, -1459.92]
delta_H_data_2 = [-4215.60, -2175.68, -3202.34, -2288.01, -1546.77]
delta_S_data_2 = [205.43, 95.19, 143.09, 80.63, 67.86]
# create a dataframe
dict2 = {
'Formula' : species_for_print,
'$$\Delta G_f^o\,(kJ\,mol^{-1})$$' : delta_G_data_2,
'$$\Delta H_f^o\,(kJ\,mol^{-1})$$' : delta_H_data_2,
'$$S^o\,(J\,mol^{-1}K^{-1})$$' : delta_S_data_2,
}
df2 = pd.DataFrame(dict2)
df2.loc[:, '$$\Delta G_f^o\,(kJ\,mol^{-1})$$'] = df2['$$\Delta G_f^o\,(kJ\,mol^{-1})$$'].map('{:.2f}'.format)
df2.loc[:, '$$\Delta H_f^o\,(kJ\,mol^{-1})$$'] = df2['$$\Delta H_f^o\,(kJ\,mol^{-1})$$'].map('{:.2f}'.format)
df2.loc[:, '$$S^o\,(J\,mol^{-1}K^{-1})$$'] = df2['$$S^o\,(J\,mol^{-1}K^{-1})$$'].map('{:.2f}'.format)
display(df2.style.hide_index())
| Formula | $$\Delta G_f^o\,(kJ\,mol^{-1})$$ | $$\Delta H_f^o\,(kJ\,mol^{-1})$$ | $$S^o\,(J\,mol^{-1}K^{-1})$$ |
|---|---|---|---|
| $$CaAl_2Si_2O_8$$ | -3991.86 | -4215.60 | 205.43 |
| $$Mg_2SiO_4$$ | -2056.70 | -2175.68 | 95.19 |
| $$CaMgSi_2O_6$$ | -3029.22 | -3202.34 | 143.09 |
| $$MgAl_2O_4$$ | -2163.15 | -2288.01 | 80.63 |
| $$MgSiO_3$$ | -1459.92 | -1546.77 | 67.86 |
# reaction
rxn = "$$CaAl_2Si_2O_8 + 2Mg_2SiO_4 = CaMgSi_2O_6 + MgAl_2O_4 + 2MgSiO_3$$"
# calculate the gibbs free energy change of the reaction
dG = hess_law_calculator(rxn, dict(zip(species, delta_G_data_2)))
# print the answers
print("The Gibbs free energy change of the reaction is %.2f kJ.\n%s" % (dG, spontaneity_checker(dG)))
The Gibbs free energy change of the reaction is -6.95 kJ.
∆G < 0, so the forward reaction is spontaneous.
Because \(\Delta G_r\) is negative, the reaction will proceed towards the products, to the right, so (diopside + spinel + 2 enstatite) is more stable.
References#
Lecture slide for Lecture 4 of the Chemistry for Geoscientists module
Lecture slide and Practical for Lecture 2 of the Low-Temperature Geochemistry module
White, W. (2013). Geochemistry. Wiley-Blackwell.

