Rotational Motion

Mechanics

Angular Momentum Theorem

From Newton’s second law:

\[\vec{F}=ma=m\frac{d\vec{v}}{dt}=\frac{d(m\vec{v})}{dt}\]

The product \(m\vec{v}\) is called linear momentum, written as \(\vec{p}\).

Taking the cross product of both sides with the position vector \(\vec{r}\):

\[\vec{r}\times\vec{F} = \vec{r}\times\left(\frac{d\vec{p}}{dt}\right)\]

The product \(\vec{r}\times\vec{F}\) is called the torque, denoted by \(\vec{\tau}\). From the rules of cross product, the magnitude of \(\vec{\tau}\) is given by:

\[|\tau|=rF_\theta\]

where \(F_\theta\) is the tangential component of \(\vec{F}\).

The direction of \(\vec{\tau}\) is perpendicular to the plane formed by \(r\) and \(F\).

Therefore:

\[\vec{\tau}=\vec{r}\times\frac{d\vec{p}}{dt}\]

From the product rule of differentiation:

\[\frac{d(\vec{r}\times\vec{p})}{dt}=\vec{r}\times\frac{d\vec{p}}{dt}+\frac{d\vec{r}}{dt}\times\vec{p}\]

Since \(\frac{d\vec{r}}{dt}=\vec{v}\) and \(m\vec{v}=\vec{p}\), RHS in the equation above becomes:

\[\vec{v}\times(m\vec{v})=m(\vec{v}\times\vec{v})=0\]

Thus:

\[\vec{\tau}=\frac{d(\vec{r}\times\vec{p})}{dt}\]

The product \(\vec{r}\times\vec{p}\) is defined as the angular momentum \(\vec{L}\), and this is the angular momentum theorem:

\[\vec{\tau}=\frac{d\vec{L}}{dt}\]

Moment of inertia

The moment of inertia of a body \(I\) composed of \(N\) discrete sub-bodies is defined as:

\[I=\sum_{i=1}^{N}m_ir_i^2\]

Where \(m_i\) is the mass of each sub-bodies, and \(r_i\) is the distance of those sub-bodies from the axis of rotation.

With this definition, the angular momentum equation reduces to:

\[\vec{\tau}=I\frac{d^2\theta}{dt^2}\]

where \(\frac{d^2\theta}{dt^2}\) represents angular acceleration.

For a continuous body, its moment of inertia \(I\) is defined as:

\[I=\int r^2dm=\int\rho(r)r^2dV\]

Tutorial Problem 4.5

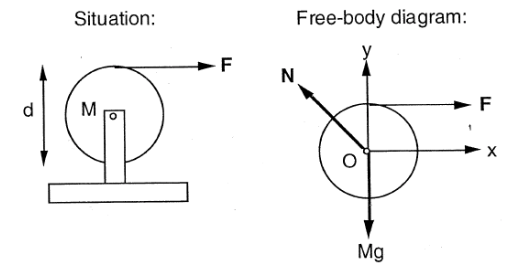
A cable is wrapped several times around a uniform, solid circular cylinder that can rotate about its axis. The cylinder has radius \(R\), and mass \(m\). The cable is pulled with a force of magnitude \(F\). Assuming that the cable unwinds without stretching or slipping, what will be the angular acceleration of the cylinder?

Ignore the weight of the cable.

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
from sympy import Symbol, integrate

F = Symbol('F') # force
M = Symbol('M') # mass of cylinder
R = Symbol('R') # distance from the centre of the cylinder to where the force is applied 
t = Symbol('t') # time

# x component of N = -F
# y component of N = Mg
# only F contributes to net torque
# sub into angular momentum equation
# for cylinder, I=MR**2/2

angular_acceleration = -(2*F)/(M*R)

angular_velocity = integrate(angular_acceleration, t)

angle = integrate(angular_velocity, t)

print("angular acceleration = ", angular_acceleration)

print("angular velocity = ", angular_velocity)

print("angle = ", angle)

angular acceleration =  -2*F/(M*R)
angular velocity =  -2*F*t/(M*R)
angle =  -F*t**2/(M*R)

# substitute arbitrary numbers
F = 10 # N
M = 10 # kg
R = 1 # m

t = np.linspace(0, 10, 500) # create list of time from 0 to 10 seconds

a_a = -(2*F)/(M*R) # angular acceleration

a_v = -2 * F * t / (M * R) # angular velocity

a = -(F * t**2) / (M * R) # angle

print("Angular acceleration = %.2f rad/s2" % (a_a))

X = R * np.cos(a) # x coordinate

Y = R * np.sin(a) # y coordinate

length = R * (-a / (2 * np.pi)) # length of string 

l = np.zeros((len(t), len(t))) # store data in matrix to make animation
for i in range(len(t)):
    for j in range(i+1):
        l[i][j] = length[j]

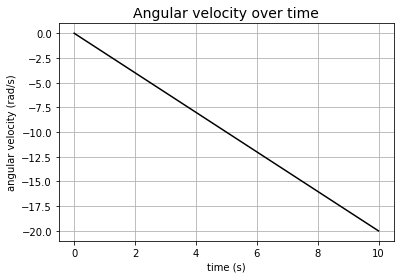
# plot angular velocity over time

fig = plt.figure(figsize=(6,4))
plt.plot(t, a_v, 'k')
plt.xlabel('time (s)')
plt.ylabel('angular velocity (rad/s)')
plt.title('Angular velocity over time', fontsize=14)
plt.grid(True)
plt.show()

Angular acceleration = -2.00 rad/s2

nframes = len(t)


# Plot background axes
fig, ax = plt.subplots(figsize=(10,2))

# plot lines
line1, = ax.plot([], [], 'ro', lw=2)
line2, = ax.plot([], [], 'k', lw=0.5)
line3, = ax.plot([], [], 'k', lw=2)


# customise axis
ax.set_xlim(-2,18)
ax.set_ylim(-2,2)
ax.set_title('Motion of cylinder and string')
    

    
lines = [line1, line2, line3]

# Plot background for each frame
def init():
    for line in lines:
        line.set_data([], [])
    return lines

# Set what data to plot in each frame
def animate(i):
    
    x1 = X[i]
    y1 = Y[i]
    lines[0].set_data(x1, y1)
    
    x2 = X
    y2 = Y
    lines[1].set_data(x2, y2)
    
    x3 = l[i]
    y3 = 1
    lines[2].set_data(x3, y3)
    
    return lines

# Call the animator
anim = animation.FuncAnimation(fig, animate, init_func=init,
                               frames=nframes, interval=10, blit=True)

HTML(anim.to_html5_video())

References

Course notes from Lecture 4 of the module ESE 95011 Mechanics